אונטערשייד צווישן ווערסיעס פון "רוי:פי"
ק (החלפת טקסט – "{{מאטעמאטיק-שטומף}}" ב־"{{שטומף|מאטעמאטיק}}") |
ק (טשעקטי און אנדערע רייניגונג, typos fixed: מדוייק ← מדויק) |
||
| שורה 41: | שורה 41: | ||
== דאס אננעמען פונעם סימבאל {{פי}} == | == דאס אננעמען פונעם סימבאל {{פי}} == | ||
[[טעקע:Leonhard_Euler.jpg|קליין|[[לעאנהארד אוילער]] האט פאפולאריזירט דעם באניץ פונעם גריכישן אות {{פי}} אין זיינע ווערק וואס ער האט פארעפנטלעכט אין 1736 און 1748.]] | [[טעקע:Leonhard_Euler.jpg|קליין|[[לעאנהארד אוילער]] האט פאפולאריזירט דעם באניץ פונעם גריכישן אות {{פי}} אין זיינע ווערק וואס ער האט פארעפנטלעכט אין 1736 און 1748.]] | ||
אין די פריעסטע באניצונגען איש דער [[גריכישער אות|גריכישער אות {{פי}}]] געווען א פארקירצונג פון דעם גריכיש ווארט פאר [[ארומנעם|פעריפעריע]] (περιφέρεια),<ref>{{Cite book|url=https://books.google.com/books?id=KTgPAAAAQAAJ&pg=PP3|title=Theorematum in libris Archimedis de sphaera et cylindro declarario|last=Oughtred|first=William|date=1652|publisher=Excudebat L. Lichfield, Veneunt apud T. Robinson|isbn=|location=|pages=|language=la|quote=δ.π :: semidiameter. semiperipheria}}</ref> און איז געווארן קאמבינירט אין פראפארציעס מיט [[דעלטע (אות)|δ]] (פאר [[דיאמעטער]]) אדער [[רהא|ρ]] (פאר [[ראדיוס]]) צו שאפן קרייז קאנסטאנטן.<ref name=":0">{{Cite book|url=https://books.google.com/?id=bT5suOONXlgC&lpg=PA9&pg=PA9|title=A History of Mathematical Notations: Vol. II|last=Cajori|first=Florian|date=2007|publisher=Cosimo, Inc.|isbn=978-1-60206-714-1|location=|pages=8–13|language=ענגליש|quote=the ratio of the length of a circle to its diameter was represented in the fractional form by the use of two letters ... J.A. Segner ... in 1767, he represented 3.14159... by δ:π, as did Oughtred more than a century earlier}}</ref><ref name=":1">{{Cite book|url=https://books.google.com/?id=uTytJGnTf1kC&lpg=PA312&pg=PA312|title=History of Mathematics|last=Smith|first=David E.|date=1958|publisher=Courier Corporation|isbn=978-0-486-20430-7|location=|pages=312|language=en}}</ref><ref>{{Cite journal|last=Archibald|first=R.C.|date=1921|title=Historical Notes on the Relation <math>e^{-(\pi/2)} = i^i</math>|jstor=2972388|journal=The American Mathematical Monthly|volume=28|issue=3|pages=116–121|doi=10.2307/2972388|quote=It is noticeable that these letters are ''never'' used separately, that is, {{פי}} is ''not'' used for 'Semiperipheria'|via=}}</ref> (פאר דעם האבן מאטעמאטיקער ווי א מאל געניצט בוכשטאבן ווי ''c'' אדער ''p'' אנשטאט דעם.<ref name="Arndt_a" />) דאס ערשטע מאל וואס איז באריכטעט איז ווען [[William Oughtred|אוטרעד]] האט געניצט "<math>\delta . \pi</math>", ארויסצודרוקן די פראפארציע פון פעריפעריע און דיאמעטער אין די 1647 און שפעטערע אויסגאבעס פון ''Clavis Mathematicae''.<ref>זעט, צום ביישפיל, {{cite book|url=https://books.google.com/books?id=ddMxgr27tNkC&pg=PA69#v=onepage&q&f=false|title=Clavis Mathematicæ|last=Oughtred|first=William|date=1648|publisher=Thomas Harper|isbn=|location=London|page=69|language=לאטיין|trans-title=דער שליסל צו מאטעמאטיק|df=dmy-all}} (איבערזעצונג אויף ענגליש : {{Cite book|url=https://books.google.com/books?id=S50yAQAAMAAJ&pg=PA99|title=Key of the Mathematics|last=Oughtred|first=William|date=1694|publisher=J. Salusbury|isbn=|location=|pages=|language=ענגליש}})</ref | אין די פריעסטע באניצונגען איש דער [[גריכישער אות|גריכישער אות {{פי}}]] געווען א פארקירצונג פון דעם גריכיש ווארט פאר [[ארומנעם|פעריפעריע]] (περιφέρεια),<ref>{{Cite book|url=https://books.google.com/books?id=KTgPAAAAQAAJ&pg=PP3|title=Theorematum in libris Archimedis de sphaera et cylindro declarario|last=Oughtred|first=William|date=1652|publisher=Excudebat L. Lichfield, Veneunt apud T. Robinson|isbn=|location=|pages=|language=la|quote=δ.π :: semidiameter. semiperipheria}}</ref> און איז געווארן קאמבינירט אין פראפארציעס מיט [[דעלטע (אות)|δ]] (פאר [[דיאמעטער]]) אדער [[רהא|ρ]] (פאר [[ראדיוס]]) צו שאפן קרייז קאנסטאנטן.<ref name=":0">{{Cite book|url=https://books.google.com/?id=bT5suOONXlgC&lpg=PA9&pg=PA9|title=A History of Mathematical Notations: Vol. II|last=Cajori|first=Florian|date=2007|publisher=Cosimo, Inc.|isbn=978-1-60206-714-1|location=|pages=8–13|language=ענגליש|quote=the ratio of the length of a circle to its diameter was represented in the fractional form by the use of two letters ... J.A. Segner ... in 1767, he represented 3.14159... by δ:π, as did Oughtred more than a century earlier}}</ref><ref name=":1">{{Cite book|url=https://books.google.com/?id=uTytJGnTf1kC&lpg=PA312&pg=PA312|title=History of Mathematics|last=Smith|first=David E.|date=1958|publisher=Courier Corporation|isbn=978-0-486-20430-7|location=|pages=312|language=en}}</ref><ref>{{Cite journal|last=Archibald|first=R.C.|date=1921|title=Historical Notes on the Relation <math>e^{-(\pi/2)} = i^i</math>|jstor=2972388|journal=The American Mathematical Monthly|volume=28|issue=3|pages=116–121|doi=10.2307/2972388|quote=It is noticeable that these letters are ''never'' used separately, that is, {{פי}} is ''not'' used for 'Semiperipheria'|via=}}</ref> (פאר דעם האבן מאטעמאטיקער ווי א מאל געניצט בוכשטאבן ווי ''c'' אדער ''p'' אנשטאט דעם.<ref name="Arndt_a" />) דאס ערשטע מאל וואס איז באריכטעט איז ווען [[William Oughtred|אוטרעד]] האט געניצט "<math>\delta . \pi</math>", ארויסצודרוקן די פראפארציע פון פעריפעריע און דיאמעטער אין די 1647 און שפעטערע אויסגאבעס פון ''Clavis Mathematicae''.<ref name="Arndt_a" /><ref>זעט, צום ביישפיל, {{cite book|url=https://books.google.com/books?id=ddMxgr27tNkC&pg=PA69#v=onepage&q&f=false|title=Clavis Mathematicæ|last=Oughtred|first=William|date=1648|publisher=Thomas Harper|isbn=|location=London|page=69|language=לאטיין|trans-title=דער שליסל צו מאטעמאטיק|df=dmy-all}} (איבערזעצונג אויף ענגליש : {{Cite book|url=https://books.google.com/books?id=S50yAQAAMAAJ&pg=PA99|title=Key of the Mathematics|last=Oughtred|first=William|date=1694|publisher=J. Salusbury|isbn=|location=|pages=|language=ענגליש}})</ref> אזוי אויך האט [[Isaac Barrow|בארא]] געניצט "<math display="inline">\frac \pi \delta</math>" צו רעפרעזענטירן דעם קאנסטאנט 3.14...,<ref>{{Cite book|chapter-url=https://archive.org/stream/mathematicalwor00whewgoog#page/n405/mode/1up|title=The mathematical works of Isaac Barrow ..|last=Barrow|first=Isaac|date=1860|publisher=Cambridge University press|others=הארווארד אוניווערסיטעט|isbn=|editor-last=Whewell|editor-first=William|location=|pages=381|language=לאטיין|chapter=Lecture XXIV}}</ref> און גרעגארי האט געניצט "<math display="inline">\frac \pi \rho</math>" צו רעפרעזענטירן 6.28... .<ref name=":1" /><ref>{{Cite journal|last=Gregorii|first=Davidis|date=1695|title=Davidis Gregorii M.D. Astronomiae Professoris Sauiliani & S.R.S. Catenaria, Ad Reverendum Virum D. Henricum Aldrich S.T.T. Decanum Aedis Christi Oxoniae|jstor=102382|journal=Philosophical Transactions|language=לאטיין|volume=19|pages=637–652}}</ref> | ||
== פי אין יידישע מקורות == | == פי אין יידישע מקורות == | ||
אין [[ספר מלכים]] ({{תנ"ך|מלכים א|ז|כג|ללא=ספר}}) איז משמע פונעם פסוק וועגן דעם ים־הנחושת וואס שלמה המלך האט געמאכט אז דער ארומנעם איז 3 מאל דעם דיאמעטער. {{ציטירן|תוכן=ויעש את הים מוצק עשר באמה משפתו עד שפתו עגול סביב וחמש באמה קומתו וקוה ([[קרי וכתיב|קרי]]: וקו) שלושים באמה יסוב אותו סביב.}} | אין [[ספר מלכים]] ({{תנ"ך|מלכים א|ז|כג|ללא=ספר}}) איז משמע פונעם פסוק וועגן דעם ים־הנחושת וואס שלמה המלך האט געמאכט אז דער ארומנעם איז 3 מאל דעם דיאמעטער. {{ציטירן|תוכן=ויעש את הים מוצק עשר באמה משפתו עד שפתו עגול סביב וחמש באמה קומתו וקוה ([[קרי וכתיב|קרי]]: וקו) שלושים באמה יסוב אותו סביב.}} | ||
{{ציטירן|תוכן=''און ער האָט געמאַכט דעם ים, אַ געגאָסענעם, צען אײלן פון ראַנד צו ראַנד, קײלעכדיק רונד אַרום, און פינף אײלן זײן הײך; און אַ שנור פון דרײסיק אײלן האָט אים אַרומגערינגלט רונד אַרום.''}} | {{ציטירן|תוכן=''און ער האָט געמאַכט דעם ים, אַ געגאָסענעם, צען אײלן פון ראַנד צו ראַנד, קײלעכדיק רונד אַרום, און פינף אײלן זײן הײך; און אַ שנור פון דרײסיק אײלן האָט אים אַרומגערינגלט רונד אַרום.''}} | ||
פשטות נעמט מען אָן אז דער פסוק איז נישט צופיל מדייק דעם נומער, און דאס הייסט נישט אז מ'האט נישט געוואוסט א מער | פשטות נעמט מען אָן אז דער פסוק איז נישט צופיל מדייק דעם נומער, און דאס הייסט נישט אז מ'האט נישט געוואוסט א מער מדויק'ן ווערט פאר <math>\ \pi</math> אין יענע צייטן, אדער אפשר איז גערעכענט דער דרויסענדיגער ארומנעם און דער אינעוועניגסטער ראדיוס. דער [[ווילנער גאון]] זאגט אז ס'איז מרומז אין פסוק די פראפארציע צווישן <math>\ \pi</math>און 3, וואס דארף אויסקומען בערך 1.04719, ווייל ס'איז דא א [[קרי וכתיב]] פונעם ווארט וואס איז געשריבן '''קוה''' און מען לייענט עס '''קו'''; די פראפארציע צווישן דער [[גימטריא]] פונעם ווארט קוה (111) און דעם ווארט קו (106) איז אומגעפער ...1.04716.{{הערה|בועז צבאן ודוד גרבר, [http://www.cs.biu.ac.il/~tsaban/Pdf/exactpi.pdf ערכים מדויקים של פאי במקורות היהדות]}} | ||
== פארמלען וואס ניצן <math>\ \pi</math> ==<!-- אין להציג את פאי באמצעות תגית <math> באמצע כותרות מסיבה תוכנית (הטקסט המתמטי לא יופיע בתוכן העניינים) --> | == פארמלען וואס ניצן <math>\ \pi</math> ==<!-- אין להציג את פאי באמצעות תגית <math> באמצע כותרות מסיבה תוכנית (הטקסט המתמטי לא יופיע בתוכן העניינים) --> | ||
| שורה 137: | שורה 137: | ||
{{רעפליסטע | {{רעפליסטע | ||
|refs= | |refs= | ||
<ref name="Newton">{{harvnb|Arndt|Haenel|2006|p=188}}. Newton quoted by Arndt.</ref> | |||
<ref name="Arndt_a">{{harvnb|Arndt|Haenel|2006|p=166}}</ref> | <ref name="Arndt_a">{{harvnb|Arndt|Haenel|2006|p=166}}</ref> | ||
}} | }} | ||
| שורה 145: | שורה 145: | ||
[[קאַטעגאָריע:נומערן]] | [[קאַטעגאָריע:נומערן]] | ||
[[ | [[קאַטעגאָריע:אומבאקוקט]] | ||
[[ | [[קאַטעגאָריע:אויף יידיש]] | ||
{{קרד/ויקי/יידיש}} | {{קרד/ויקי/יידיש}} | ||
רעוויזיע פון 22:36, 8 דעצעמבער 2022
הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \pi} (דער גריכישער אות פי) איז א מאטעמאטישער קאנסטאנט, א רעאלע צאל וואס איר ווערט איז די פראפארציע (אין אוקלידישער געאמעטריע) צווישן דעם ארומנעם פון א קרייז צו זיין דיאמעטער. מען ניצט π ווייל ער איז דער ערשטער אות פונעם גריכישן ווארט "περίμετρος" (פערימעטראס) וואס מיינט ארומנעם.
די ערשטע 50 ציפערן אין דער אומענדיקער דעצימאלער רעפרעזענטאציע פון הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \pi} זענען: 3.14159265358979323846264338327950288419716939937510.
דאס איז א אומראציאנעלער נומער, ד. ה. אז עס איז נישט מעגליך צו דאס ארויסברענגען ווי א פראפארציע פון צוויי גאנצע נומערן. דאס האט לאמבערט דערוויזן אין יאר 1761. אבער, מען רעפרעזענטירט הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \pi} ווי א פראקציע, למשל 22/7.
אין יאר 1882 האט פערדינאנד לינדעמאן באוויזן דעם לינדעמאן־ווייערשטראס טעארעם פון וואס עס ווערט געדרונגען אז הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \ \pi} איז א טראנסצענדענטישע צאל.[1] פון דעם באווייז קומט אויס אז מען קען נישט ווייזן הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \ \pi} מיט אן ענדלעכע צאל פון גאנצע צאלן, ברוכצאלן, אדער זייערע ווארצלען, צוזאמען מיט די פיר הויפט־פעולות פון חשבון. איין רעזולטאט פון דעם טעארעם איז אז מען קען נישט, ניצנדיק א ווירע און א צירקל, שאפן א קוואדראט מיט דעם גלייכן שטח ווי א געוויסער קרייז, איינער פון די קלאסישע פראבלעמען פון מאטעמאטיק.
ווייל די עלעמענטארסטע דעפיניציע פון הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \ \pi} האט א שייכות מיט דעם קרייז, געפינט זיך הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \ \pi} אין עטלעכע פארמלען אין טריגאנאמעטריע און געאמעטריע, ספעציעל די וואס האבן צו טון מיט קרייזן, עליפסן און קיילעכן. אין מער מאדערנעם מאטעמאטישן אנאליז, ווערט דער דעפינירט אנדערש ניצנדיק די ספעקטראלע אייגנשאפטן פון דער רעאלע צאל סיסטעם, ווי אן אייגנווערט אדער פעריאד, אן קיין שום רעפערענץ צו געאמעטריע. דערפאר באווייזט זיך הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \ \pi} אין טיילן פון מאטעמאטיק און וויסנשאפטן וואס קיין שייכות נישט מיט דער געאמעטריע פון קרייזן, ווי למשל נומערן טעאריע און סטאטיסטיק, ווי אויך אין כמעט אלע געביטן פון פיזיק. צוליב דער אומעטומקייט פון הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \ \pi} איז ער איינער פון די מערסט באוואוסטע מאטעמאטישע קאנסטאנטן סיי אינערהאלב סיי אינדרויסן פון דער וויסנשאפטלעכער געמיינדע. עס זענען פאראן גאנצע ביכער וועגן הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \ \pi} , און מען האט שוין גערעכנט וואס מער ציפערן פון הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \ \pi} . מענטשן האבן שוין זיך אויסגעלערנט הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \ \pi} צו מער ווי 70,000 ציפערן.
אייגנשאפטן
הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \ \pi} איז אן אומראציאנעלע צאל, ד"ה מען קען אים נישט שרייבן ווי א ברוכצאל פון צוויי גאנצע צאלן. די אייגנשאפט איז באוויזן געווארן אין יאר 1761 דורך יאהאן היינריך לאמבערט.[2]
אין יאר 1882 האט פערדינאנד לינדעמאן באוויזן דעם לינדעמאן טעארעם פון וואס עס קומט ארויס דירעקט אז הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \ \pi} איז א טרנסצענדענטאלע צאל.[1] פון דעם באווייז קומט אויס אז הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \ \pi} קען נישט ווערן גערעכנט פון גאנצע צאלן, ברוכצאלן אדער זייערע ווארצלען צוזאמען מיט די פיר פעולות פון חשבון. נאך אן אויסקום איז אז מען קען נישט, דורך קאנסטרוקציע מיט א ווירע און א צירקל, שאפן א קוואדראט וואס זיין שטח איז גלייך צום שטח פון א געגעבענעם קרייז – איינער פון די קלאסישע פראבלעמען פון געאמעטריע.
רעכענען π
רעכענען א מער און מער גענויען ווערט פאר הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \ \pi} איז געווארן אן ארויסרוף במשך הונדערטער יאר.
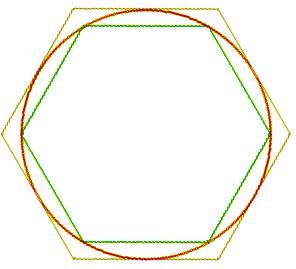
מען האט געוואוסט בערכדיקע ווערטן צו פי שוין אין בבל און אין אוראלט עגיפטן, אבער ארכימעד האט געוויזן צום ערשטן מאל א מעטאד וואס דערמעגלעכט רעכענען הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \ \pi} צו נארוועלכער גענויקייט (דער אויסשעפונג מעטאד). דער מעטאד איז באזירט אויף דעם וואס דער ארומנעם פון דעם קרייז איז קלענער ווי דער ארומנעם פון דעם פילעק וואס דער קרייז איז זיין אינקרייז, און גרעסער ווי דער ארומנעם פון דעם פילעק וואס דער קרייז איז זיין ארומקרייז. מיטן רעכענען דעם ארומנעם פון די ביידע פילעקן, וואס דער פילעק קען האבן וואס מער ריפן, קען מען רעכענען דעם ארומנעם פונעם קרייז וואס מער גענוי, און במילא רעכענען הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \ \pi} וואס מער גענוי. ארכימעד האט געניצט זיין מעטאד מיט א זעקסעק, און דערנאך האט ער געטאפלט די צאל ריפן (ניצנדיק כסדר רעגלמעסיקע פילעקן). מיט א פילעק פון 96 ריפן האט ארכימעד געקומען צום ארויסקום [3] (וואס דערשיינט אינעם בוך וועגן מעסטן דעם קרייז):
הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle 3\frac{10}{71} < \pi < 3\frac{1}{7}}
בערך יאר 480 האט דער כינעזישער מאטעמאטיקער זו טשאנגזשי גערעכנט אז π ≈ הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{355}{113}} ניצנדיק א פילעק מיט 12,288 עקן. דער ווערט 3.141592920 איז געהעריג אין די ערשטע זיבן ציפערן, און האט געהאלטן 800 יאר.
אין דעם אנהייב פונעם 15טן יארהונדערט האט דער פערסישער מאטעמאטיקער און אסטראנאם אל-קאשי גערעכנט הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \ 2\pi} צו 9 ציפערן אין דעם סעקסיגעסימאל-באזע, א גענויקייט וואס איז גלייך צו 16 ציפערן אין דעצימאל.
אין יאר 1596 האט דער האלענדער לודאלף וואן קעלין דערגרייכט 20 ציפערן, און עטלעכע יאר נאכהער האט ער דערגרייכט א גענויקייט פון 35 ציפערן.
די אנטוויקלונג פון דעם קאלקולוס אין דעם 17טן יארהונדערט האט געברענגט נייע סיסטעמען צו רעכענע הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \ \pi} . די סיסטעמען זענען באזירט אויף א רעפרעזענטאציע פון הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \ \pi} ווי דער סכום פון אן אומענדלעכער סעריע.
אומענדלעכע סעריעס
די רעכענונג פון π איז געווארן רעוואלוציאנירט דורך דער אנטוויקלונג פון אומענדלעכע סעריע טעכניקן אין די 16טע און 17טע יארהונדערטער. און אומענדלעכע סעריע איז דער צוגאב פון די עלעמענטן פון אן אומענדלעכן סעקווענץ.[5] אומענדעלעכע סעריעס האבן געלאזט מאטעמאטיקער רעכענען הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \ \pi} מיט פיל גרעסערער פרעציזקייט ווי ארכימעד און אנדערע וואס האבן געניצט געאמעטרישע טעכניקן.[5] כאטש מען האט אויסגעניצט אומענדלעכע סעריעס פאר π, איבערהויפט דורך אייראפעאישע מאטעמאטיקער ווי דזשיימס גרעגארי און גאטפריד ווילהעלם לייבניץ, דעם דאזיגן צוגאנג האט מען שוין אנטפלעקט אין אינדיע צווישן די יארן 1400 און 1500 צו דער ציווילער רעכענונג.[6] די ערשטע געשריבענע באשרייבונג פון אן אומענדלעכער סעריע וואס מ'האט געקענט ניצן צו רעכענען π איז געווען אויסגעלייגט אין סאנסקריט פערזן דורך דעם אינדישן אסטראנאם נילאקאנטא סאמאיאדזשי אין זיין טאנטראסאמגראהא, בערך אין יאר 1500.[7] די סעריעס ווערן געברענגט אן קיין באווייזונג, אבער עס קומען פאר באווייזן אין א שפעטערדיקער אינדישער ווערק, יוקטיבאהאסא, פון בערך יאר 1530. נילאקאנטא שרייבט צו די סעריעס צו א פריערדיקן אינדישן מאטעמאטיקער, מאדהאווא פון סאנגאמאגראמא, וואס האט געלעבט אומגעפער 1350 – 1425.[7] עטלעכע אומענדלעכע סעריעס ווערן באשריבן, איינשליסנדיק סעריעס פאר סינוס, טאנגענס און קאסינוס, וואס מען רופט היינט די מאדהאווא סעריע אדער גרעגארי–לייבניץ סעריע.[7] מאדהאווא האט געניצט אומענדלעכע סעריעס צו שאצן π ביז 11 ציפערן ארום יאר 1400, אבער ארום 1430 האט דער פערסישער מאטעמאטיקער דזשאמשיד אל-קאשי פארבעסערט די רעכענונג, מיט א פילעק־אלגאריטם.[8]
דאס אננעמען פונעם סימבאל π

אין די פריעסטע באניצונגען איש דער גריכישער אות π געווען א פארקירצונג פון דעם גריכיש ווארט פאר פעריפעריע (περιφέρεια),[9] און איז געווארן קאמבינירט אין פראפארציעס מיט δ (פאר דיאמעטער) אדער ρ (פאר ראדיוס) צו שאפן קרייז קאנסטאנטן.[10][11][12] (פאר דעם האבן מאטעמאטיקער ווי א מאל געניצט בוכשטאבן ווי c אדער p אנשטאט דעם.[13]) דאס ערשטע מאל וואס איז באריכטעט איז ווען אוטרעד האט געניצט "הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \delta . \pi} ", ארויסצודרוקן די פראפארציע פון פעריפעריע און דיאמעטער אין די 1647 און שפעטערע אויסגאבעס פון Clavis Mathematicae.[13][14] אזוי אויך האט בארא געניצט "הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\textstyle \frac \pi \delta} " צו רעפרעזענטירן דעם קאנסטאנט 3.14...,[15] און גרעגארי האט געניצט "הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\textstyle \frac \pi \rho} " צו רעפרעזענטירן 6.28... .[11][16]
פי אין יידישע מקורות
אין ספר מלכים (ז, כג) איז משמע פונעם פסוק וועגן דעם ים־הנחושת וואס שלמה המלך האט געמאכט אז דער ארומנעם איז 3 מאל דעם דיאמעטער.
ויעש את הים מוצק עשר באמה משפתו עד שפתו עגול סביב וחמש באמה קומתו וקוה (קרי: וקו) שלושים באמה יסוב אותו סביב.
און ער האָט געמאַכט דעם ים, אַ געגאָסענעם, צען אײלן פון ראַנד צו ראַנד, קײלעכדיק רונד אַרום, און פינף אײלן זײן הײך; און אַ שנור פון דרײסיק אײלן האָט אים אַרומגערינגלט רונד אַרום.
פשטות נעמט מען אָן אז דער פסוק איז נישט צופיל מדייק דעם נומער, און דאס הייסט נישט אז מ'האט נישט געוואוסט א מער מדויק'ן ווערט פאר הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \ \pi} אין יענע צייטן, אדער אפשר איז גערעכענט דער דרויסענדיגער ארומנעם און דער אינעוועניגסטער ראדיוס. דער ווילנער גאון זאגט אז ס'איז מרומז אין פסוק די פראפארציע צווישן הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \ \pi} און 3, וואס דארף אויסקומען בערך 1.04719, ווייל ס'איז דא א קרי וכתיב פונעם ווארט וואס איז געשריבן קוה און מען לייענט עס קו; די פראפארציע צווישן דער גימטריא פונעם ווארט קוה (111) און דעם ווארט קו (106) איז אומגעפער ...1.04716.[17]
פארמלען וואס ניצן הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \ \pi}
פי באווייזט זיך אין פיל מאטעמאטישע פארמלען. פארשטייט זיך אז פארמלען וואס מעסטן קרייזן און ספערן ניצן הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \ \pi} , אבער אויך אין גאר אנדערע געביטן וואס האבן אייגנטלעך נישט קיין שייכות מיט געאמעטריע אדער קרייזן.
געאמעטריע
| ארומנעם פון א קרייז | הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle C = 2 \pi r \,\!} |
| שטח פון א קרייזפלאך | הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle A = \pi r^2 \,\!} |
| שטח פון אן עליפס | הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle A = \pi a b \,\!} |
| פארנעם פון א קיילעך | הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle V = \frac{4\pi r^3}{3} \,\!} |
| אייבערפלאך שטח פון א קיילעך | הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle A = 4 \pi r^2 \,\!} |
| פארנעם פון א צילינדער | הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle V = \pi r^2 h \,\!} |
| אייבערפלאך שטח פון א צילינדער | הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle A = 2 ( \pi r^2 ) + ( 2 \pi r ) h = 2 \pi r (r + h) \,\!} |
| פארנעם פון א קאנוס | הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle V = \frac{\pi r^2 h}{3} \,\!} |
| אייבערפלאך שטח פון א קאנוס | הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle A = \pi r \sqrt{r^2 + h^2} + \pi r^2 = \pi r (r + \sqrt{r^2 + h^2}) \,\!} |
מאטעמאטישער אנאליז
- הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac2\pi= \frac{\sqrt2}2 \frac{\sqrt{2+\sqrt2}}2 \frac{\sqrt{2+\sqrt{2+\sqrt2}}}2\ldots}
- גרעגארי-לייבניץ פארמל, אויף די נעמען פון דזשיימס גרעגארי (1638–1675) און ווילהעלם לייבניץ. גרעגארי האט אנטפלעקט די פארמל אין 1672. זי דערשיינט אויך אין דעם בוך Ganita-Yukti-Bhasa וואס דער אינדישער מאטעמאטיקער Jyesthadeva האט געשריבן אין דעם 16טן יארהונדערט. די פארמל איז
- הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{1} - \frac{1}{3} + \frac{1}{5} - \frac{1}{7} + \frac{1}{9} - \cdots = \frac{\pi}{4}}
- ד"ה:
- הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sum_{n=1}^{\infty} (-1)^{n-1} \left (\frac{1}{2n-1}\right ) = \frac{\pi}{4}}
- (מען באקומט די סעריע ווען מען שטעלט הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \ x=1} אין דער טיילאר סעריע פאר הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \ \arctan(x)} )
- דער וואליס פראדוקט:
- הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{2}{1} \cdot \frac{2}{3} \cdot \frac{4}{3} \cdot \frac{4}{5} \cdot \frac{6}{5} \cdot \frac{6}{7} \cdot \frac{8}{7} \cdot \frac{8}{9} \cdots = \frac{\pi}{2} }
- דער אינטעגראל פון דער גאוס פונקציע (נארמאלע פארטיילונג):
- הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \int_{-\infty}^{\infty} e^{-x^2}\,dx = \sqrt{\pi}}
- דער באזעלער פראבלעם וואס לעאנהארד אוילער האט געלייזט (זעט אויך די רימאן זעטא פונקציע):
- הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \zeta(2) = \frac{1}{1^2} + \frac{1}{2^2} + \frac{1}{3^2} + \frac{1}{4^2} + \cdots = \frac{\pi^2}{6}}
- הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \zeta(4)= \frac{1}{1^4} + \frac{1}{2^4} + \frac{1}{3^4} + \frac{1}{4^4} + \cdots = \frac{\pi^4}{90}}
- די גאמא פונקציע (וואס איז א גענעראליזאציע פון דער פאקטאריאל פונקציע) פון 1/2:
- הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Gamma\left({1 \over 2}\right)=\sqrt{\pi}}
- סטירלינג פארמל וואס מען ניצט צו דערנענטערן דעם פאקטאריאל פון גרויסע צאלן:
- הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle n! \sim \sqrt{2 \pi n} \left(\frac{n}{e}\right)^n}
- (מען באווייזט די טענה דורך אן אסימפטאטישע אנטוויקלונג פון דער גאמא פונקציע)
- די אוילער אידענטיטעט וואס איז באזירט אויף דער אוילער פארמל (וואס ריטשארד פיינמאן האט גערופן די "וואונדערבארסטע אידענטיטעט אין מאטעמטיק", און זי פארבינדט די פינף פונדאמענטאלע מאטעמאטישע קאנסטאנטן):
- הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle e^{\pi i} + 1 = 0\;}
- דער שטח פון א קוואדראט פון דעם איינץ-קרייז:
- הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \int_0^1 \sqrt{1-x^2}\ dx = {\pi \over 4}}
- נאך אן אומאייגנטלעכער אינטעגראל:
- הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \int_{-\infty}^{\infty} \frac{1}{x^2 + 1}\,dx = \pi}
רעפערענצן
- ↑ 1.0 1.1 Mayer, Steve. "The Transcendence of π". Archived from the original on 2000-09-29. Retrieved 4טן נאוועמבער 2007
{{cite web}}: Check date values in:|accessdate=(help). - ↑ זעט באווייזן אין דעם ארטיקל Proof that π is irrational אין דעם ענגליש-וויקיפעדיע.
- ↑ א פראגראם וואס מוסטערט ארכימעד'ס מעטאד באשיינט אויפן וועבזייטל Archimedes and the Computation of Pi.
- ↑ ציטירן פאנטשער: אומגילטיגער
<ref>טעג; קיין טעקסט נישט געשריבן פאַר רעפערענצן מיטן נאָמעןNewton - ↑ 5.0 5.1 Arndt & Haenel 2006, pp. 185–191
- ↑ Roy 1990, pp. 101–102 Arndt & Haenel 2006, pp. 185–186
- ↑ 7.0 7.1 7.2 Roy 1990, pp. 101–102
- ↑ Joseph 1991, p. 264
- ↑ Oughtred, William (1652). Theorematum in libris Archimedis de sphaera et cylindro declarario (in לאטייניש). Excudebat L. Lichfield, Veneunt apud T. Robinson.
δ.π :: semidiameter. semiperipheria
- ↑ Cajori, Florian (2007). A History of Mathematical Notations: Vol. II (in ענגליש). Cosimo, Inc. pp. 8–13. ISBN 978-1-60206-714-1.
the ratio of the length of a circle to its diameter was represented in the fractional form by the use of two letters ... J.A. Segner ... in 1767, he represented 3.14159... by δ:π, as did Oughtred more than a century earlier
- ↑ 11.0 11.1 Smith, David E. (1958). History of Mathematics (in ענגליש). Courier Corporation. p. 312. ISBN 978-0-486-20430-7
- ↑ Archibald, R.C. (1921). "Historical Notes on the Relation הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle e^{-(\pi/2)} = i^i}
". The American Mathematical Monthly. 28 (3): 116–121. doi:10.2307/2972388. JSTOR 2972388.
It is noticeable that these letters are never used separately, that is, π is not used for 'Semiperipheria'
- ↑ 13.0 13.1 ציטירן פאנטשער: אומגילטיגער
<ref>טעג; קיין טעקסט נישט געשריבן פאַר רעפערענצן מיטן נאָמעןArndt_a - ↑ זעט, צום ביישפיל, Oughtred, William (1648). Clavis Mathematicæ [דער שליסל צו מאטעמאטיק] (in לאטיין). London: Thomas Harper. p. 69
{{cite book}}: CS1 maint: unrecognized language (link) (איבערזעצונג אויף ענגליש : Oughtred, William (1694). Key of the Mathematics (in ענגליש). J. Salusbury) - ↑ Barrow, Isaac (1860). "Lecture XXIV". In Whewell, William (ed.). The mathematical works of Isaac Barrow . (in לאטיין). הארווארד אוניווערסיטעט. Cambridge University press. p. 381
{{cite book}}: CS1 maint: unrecognized language (link) - ↑ Gregorii, Davidis (1695). "Davidis Gregorii M.D. Astronomiae Professoris Sauiliani & S.R.S. Catenaria, Ad Reverendum Virum D. Henricum Aldrich S.T.T. Decanum Aedis Christi Oxoniae". Philosophical Transactions (in לאטיין). 19: 637–652. JSTOR 102382
{{cite journal}}: CS1 maint: unrecognized language (link) - ↑ בועז צבאן ודוד גרבר, ערכים מדויקים של פאי במקורות היהדות.
דאס איז נישט קיין המכלול ארטיקל, בלויז עפעס וואס ליגט דא ביז עס וועט ערזעצט ווערן מיט בעסערס. שרייבט עס איבער!