אונטערשייד צווישן ווערסיעס פון "רוי:מאטעמאטיק"
ק (החלפת טקסט – "וויכטיקייט" ב־"וויכטיגקייט") |
|||
| (9 מיטלסטע ווערסיעס פון 5 באַניצער נישט געוויזן.) | |||
| שורה 1: | שורה 1: | ||
{{דעסקריפציע|די וויסנשאפט וואס פארנעמט זיך מיט צאלן און פארמען}} | |||
'''מאַטעמאַטיק''' איז די [[וויסנשאפט]] וואס פארנעמט זיך מיט [[נומערן סיסטעם|צאלן]] און [[פארעם|פארמען]]. מאטעמאטיק מיינט רעכענען, [[ציילן]], און [[מאס|מעסטן]]. די אפטייל וואס באשעפטיגט זיך מיט פארמען און מאסן הייסט [[געאמעטריע]]. די וועג צו אויסגעפינען מאטעמאטיקס-פראבלעמען ווערט געטון דורך [[פארמולע]]ן. | '''מאַטעמאַטיק''' איז די [[וויסנשאפט]] וואס פארנעמט זיך מיט [[נומערן סיסטעם|צאלן]] און [[פארעם|פארמען]]. מאטעמאטיק מיינט רעכענען, [[ציילן]], און [[מאס|מעסטן]]. די אפטייל וואס באשעפטיגט זיך מיט פארמען און מאסן הייסט [[געאמעטריע]]. די וועג צו אויסגעפינען מאטעמאטיקס-פראבלעמען ווערט געטון דורך [[פארמולע]]ן. | ||
[[טעקע:Newton-Principia-Mathematica 1-500x700.jpg|קליין|אייזיק ניוטאן, ''פרינקיפיא מאטעמאטיקא'' (שער בלאט)]] | [[טעקע:Newton-Principia-Mathematica 1-500x700.jpg|קליין|אייזיק ניוטאן, ''פרינקיפיא מאטעמאטיקא'' (שער בלאט)]] | ||
| שורה 4: | שורה 5: | ||
דער וואס באשעפטיגט זיך מיט מאטעמאטיק, צי ווי א לערע אדער ווי א האבי, הייסט א '''מאטעמאטיקער'''. | דער וואס באשעפטיגט זיך מיט מאטעמאטיק, צי ווי א לערע אדער ווי א האבי, הייסט א '''מאטעמאטיקער'''. | ||
אין [[אקאדעמיע]], איז מאטעמאטיק אן אפטייל פון די [[ | אין [[אקאדעמיע]], איז מאטעמאטיק אן אפטייל פון די [[פינקטליכע וויסנשאפט]]. מיט די לערע קען מען פארשן [[פיזיק]], [[כעמיע]], [[אסטראנאמיע]], [[סטאטיסטיק]] און נאך. אויך אין דעם [[לעבנסשטייגער]] ניצט מען זיך מיט מאטעמאטיק אויף [[האנדל]] און [[ביזנעס]]. | ||
[[קארל פרידריך גאוס]] (1777–1855) האט גערופן מאטעמאטיק "די מלכה פון די וויסנשאפטן". | [[קארל פרידריך גאוס]] (1777–1855) האט גערופן מאטעמאטיק "די מלכה פון די וויסנשאפטן". | ||
| שורה 12: | שורה 13: | ||
מאטעמאטיק אנטוויקלט זיך דורך דריי כאראקטעריסטיקן: [[אבסטראקציע (מאטעמאטיק)|אבסטראקציע]], [[גענעראליזאציע]] און [[מאטעמאטישער דערווייז|דערווייז]]. | מאטעמאטיק אנטוויקלט זיך דורך דריי כאראקטעריסטיקן: [[אבסטראקציע (מאטעמאטיק)|אבסטראקציע]], [[גענעראליזאציע]] און [[מאטעמאטישער דערווייז|דערווייז]]. | ||
מאטעמאטיק איז א | מאטעמאטיק איז א לעבנסנויטיגער געצייג אין פארשידענע געביטן, איינשליסנדיק [[נאטור-וויסנשאפטן]], [[אינזשעניריע]], [[מעדיצין]] און געוויסע [[סאציאל וויסנשאפט]]ן ווי [[עקאנאמיק]] און [[פסיכאלאגיע]]. פראבלעמען וואס שטאמען פון אנדערע וויסנשאפט צווייגן זענען א קאטאליזאטאר פאר נייע מאטעמאטיקע אויסגעפינען, און טיילמאל אפילו נייע מאטעמאטישע געביטן. | ||
[[אנגעווענדעטע מאטעמאטיק]], די צווייג פון מאטעמאטיק וואס באהאנדלט די אנווענדונג פון מאטעמאטישן וויסן צו אנדערע פעלדער, אינספירירט און ניצט נייע מאטעמאטישע אויספינדונגען, ברענגנדיק די אנטוויקלונג פון נייע מאטעמאטישע דיסציפלינען, ווי למשל [[סטאטיסטיק]] און [[שפיל טעאריע]]. אויך פארנעמען זיך מאטעמאטיקער מיט [[ריינע מאטעמאטיק]], אן קיין שום קלער פון אן אנווענדונג. | [[אנגעווענדעטע מאטעמאטיק]], די צווייג פון מאטעמאטיק וואס באהאנדלט די אנווענדונג פון מאטעמאטישן וויסן צו אנדערע פעלדער, אינספירירט און ניצט נייע מאטעמאטישע אויספינדונגען, ברענגנדיק די אנטוויקלונג פון נייע מאטעמאטישע דיסציפלינען, ווי למשל [[סטאטיסטיק]] און [[שפיל טעאריע]]. אויך פארנעמען זיך מאטעמאטיקער מיט [[ריינע מאטעמאטיק]], אן קיין שום קלער פון אן אנווענדונג. | ||
| שורה 26: | שורה 27: | ||
נייע מאטעמאטישע אויסגעפינען זענען געווארן אנטדעקט דורכאויס דער היסטאריע, און ווערן נאכאלץ אנטדעקט ביזן היינטיגן טאג. די אנטוויקלונג פון מאטעמאטיק אין [[אוראלטע היסטאריע|אוראלטע צייטן]] האט דערגרייכט איר שפיץ און [[אוראלט גריכנלאנד]], א דאנק די בארימטע מאטעמאטיקער ווי [[אוקלידוס]] און [[ארכימעד]]. | נייע מאטעמאטישע אויסגעפינען זענען געווארן אנטדעקט דורכאויס דער היסטאריע, און ווערן נאכאלץ אנטדעקט ביזן היינטיגן טאג. די אנטוויקלונג פון מאטעמאטיק אין [[אוראלטע היסטאריע|אוראלטע צייטן]] האט דערגרייכט איר שפיץ און [[אוראלט גריכנלאנד]], א דאנק די בארימטע מאטעמאטיקער ווי [[אוקלידוס]] און [[ארכימעד]]. | ||
אין דעם [[מיטל אלטער]] איז די עיקר אנטוויקלונג געווען ביי די [[אראבער]], וואס האבן אנטוויקלט [[אלגעברע]] און [[טריגאנאמעטריע]]. אינעם [[17טער י"ה|17טן יארהונדערט]] האבן געבליט פארשידענע צווייגן פון מאטעמאטיק, למשל [[אנאליטישע געאמעטריע]] און [[קאלקולוס]], וואס זענען געווארן די שפרינגברעט פאר פיל | אין דעם [[מיטל אלטער]] איז די עיקר אנטוויקלונג געווען ביי די [[אראבער]], וואס האבן אנטוויקלט [[אלגעברע]] און [[טריגאנאמעטריע]]. אינעם [[17טער י"ה|17טן יארהונדערט]] האבן געבליט פארשידענע צווייגן פון מאטעמאטיק, למשל [[אנאליטישע געאמעטריע]] און [[קאלקולוס]], וואס זענען געווארן די שפרינגברעט פאר פיל וויסנשאפטליכע צווייגן. די אנטוויקלונג פון [[נישט-אוקלידישע געאמעטריע|נישט-אוקלידישער געאמעטריע]] אינעם [[19טער י"ה|19טן יארהונדערט]] האבן אונטערגעשריכן די וויכטיגקייט פון [[אקסיאם|אקסיאמען]] אין מאטעמאטיק, אין די פארווייטערונג פון אן אינטואיטיוון צוגאנג. בים סוף פונעם 19טן יארהונדערט איז אנטוויקלט געווארן [[געזעמלען טעאריע]], און אויך האט אנטוויקלט א דעבאטע וועגן די [[פונדאמענטן פון מאטעמאטיק]]. | ||
אינעם 20סטן יארהונדערט האט מאטעמאטיק זיך אנטוויקלט גיך, מיט דער לייזונג פון מערערע פון [[דויד הילבערט|הילבערטס]] 23 פראבלעמען. | אינעם 20סטן יארהונדערט האט מאטעמאטיק זיך אנטוויקלט גיך, מיט דער לייזונג פון מערערע פון [[דויד הילבערט|הילבערטס]] 23 פראבלעמען. | ||
| שורה 40: | שורה 41: | ||
=== כמות === | === כמות === | ||
די שטודיע פון כמות (קוואַנטיטעט) הייבט אן מיט [[צאל|נומערן]], ערשט די באקאנטע [[ | די שטודיע פון כמות (קוואַנטיטעט) הייבט אן מיט [[צאל|נומערן]], ערשט די באקאנטע [[נאטירליכע צאל]] און [[גאנצע צאל]], מיט די [[אריטמעטישע אפעראציעס]] אויף זיי, וואס צוזאמען ווערן שטודירט אין [[אריטמעטיק]]. די טיפערע אייגנשאפטן פון נומערן שטודירט מען אין [[נומערן טעאריע]], פון וואנעט קומען אזעלכע רעזולטאטן ווי [[פערמא'ס לעצטער טעארעם]]. צווישן די נישט געלייזטע פראבלעמען פון נומערן טעאריע זענען די [[פרימצאל-צווילינג]] השערה און די [[גאלדבאך-השערה]]. | ||
מיט דער אנטוויקלונג פון דער נומערן־סיסטעם, אנערקענט מען די | מיט דער אנטוויקלונג פון דער נומערן־סיסטעם, אנערקענט מען די נאטירליכע צאל ווי אן אונטער־געזעמל פון די [[ראציאנאלע צאל]] ([[בראכטייל|בראכטיילן]]), וואס זיי זענען א טייל פון די [[רעאלע צאל]], מיט וואס מען קען דעפינירן [[נאכאנאנדיקע פונקציע|נאכאנאנדיקע פונקציעס]]. רעאלע צאל קען מען פארברייטערן ווייטער צו [[קאמפלעקסע צאל]]. | ||
| שורה 48: | שורה 49: | ||
| <math>1, 2, 3\,\!</math> || <math>-2, -1, 0, 1, 2\,\!</math> || <math> -2, \frac{2}{3}, 1.21\,\!</math> || <math>-e, \sqrt{2}, 3, \pi\,\!</math> || <math>2, i, -2+3i, 2e^{i\frac{4\pi}{3}}\,\!</math> | | <math>1, 2, 3\,\!</math> || <math>-2, -1, 0, 1, 2\,\!</math> || <math> -2, \frac{2}{3}, 1.21\,\!</math> || <math>-e, \sqrt{2}, 3, \pi\,\!</math> || <math>2, i, -2+3i, 2e^{i\frac{4\pi}{3}}\,\!</math> | ||
|- | |- | ||
| [[ | | [[נאטירליכע צאל]] || [[גאנצע צאל]] || [[ראציאנאלע צאל]] || [[רעאלע צאל]] || [[קאמפלעקסע צאל]] | ||
|} | |} | ||
=== סטרוקטור === | === סטרוקטור === | ||
| שורה 82: | שורה 83: | ||
=== ענדערונג === | === ענדערונג === | ||
שילדערן און פארשטיין ענדערונג איז שטארק נויטבאר אין דער [[נאטור-וויסנשאפטן]], און דער [[קאלקולוס]] איז א קראפטיגער געצייג דערפאר. דער הויפט באגריף איז די [[פונקציע]]. די שטודיע פון [[רעאלע צאל]]ן און פונקציעס וואס האבן רעאלע ווערטן הייסט [[רעאלער אנאליז]], און די פאראלעלע שטודיע פון פונקציעס פון [[קאמפלעקסע צאל]]ן הייסט [[קאמפלעקסער אנאליז]]. די [[רימאן השערה]], איינע פון די אפענע יסודותדיקע פראגעס אין מאטעמאטיק, קוואלט ארויס פון קאמפלעקסן אנאליז. [[פונקציאנאלער אנאליז]] פאקוסירט אויף פונקציע רוימען, בדרך כלל מיט | שילדערן און פארשטיין ענדערונג איז שטארק נויטבאר אין דער [[נאטור-וויסנשאפטן]], און דער [[קאלקולוס]] איז א קראפטיגער געצייג דערפאר. דער הויפט באגריף איז די [[פונקציע]]. די שטודיע פון [[רעאלע צאל]]ן און פונקציעס וואס האבן רעאלע ווערטן הייסט [[רעאלער אנאליז]], און די פאראלעלע שטודיע פון פונקציעס פון [[קאמפלעקסע צאל]]ן הייסט [[קאמפלעקסער אנאליז]]. די [[רימאן השערה]], איינע פון די אפענע יסודותדיקע פראגעס אין מאטעמאטיק, קוואלט ארויס פון קאמפלעקסן אנאליז. [[פונקציאנאלער אנאליז]] פאקוסירט אויף פונקציע רוימען, בדרך כלל מיט אומענדליכע דימענסיעס. פונקציאנאלער אנאליז ווערט געניצט אין [[קוואנטן-מעכאניק]]. עס זענען פאראן פילע פראבלעמען וואס זייער לייזונג ליגט אין א פארהעלטעניש צווישן א קוואנטיטעט און זיין ענדערונג, וואס מען שטודירט אין דעם געביט פון [[דיפערענציאל-גלייכונג]]ען. | ||
א סך פענאמענען אין נאטור קען מען שילדערן דורך [[דינאמישע סיסטעם|דינאמישע סיסטעמען]]; [[כאאס-טעאריע]] פארשט גענוי ווי די סיסטעמען ארבעטן. [[נומערישער אנאליז]] פארשט מעטאדן צו לייזן א ברייטן גרייך פון פראבלעמען וואס מען קען נישט לייזן אנאליטיש. | א סך פענאמענען אין נאטור קען מען שילדערן דורך [[דינאמישע סיסטעם|דינאמישע סיסטעמען]]; [[כאאס-טעאריע]] פארשט גענוי ווי די סיסטעמען ארבעטן. [[נומערישער אנאליז]] פארשט מעטאדן צו לייזן א ברייטן גרייך פון פראבלעמען וואס מען קען נישט לייזן אנאליטיש. | ||
| שורה 99: | שורה 100: | ||
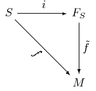
כדי צו געבן צו פארשטיין די [[פונדאמענטן פון מאטעמאטיק]] האט מען אנטוויקלט די געביטן פון [[מאטעמאטישע לאגיק|מאטעמאטישער לאגיק]] און [[געזעמלען טעאריע]], ווי אויך [[קאטעגאריע טעאריע]] וואס ווערט נאכאלץ אנטוויקלט. די פראזע "קריזיס פון פונדאמענטן" וואס באשרייבט די זוך אין אנהייב פונעם 20סטן יארהונדערט נאך פאסיקע פונדאמענטן פאר מאטעמאטיק, איז א פארציענדיקער פענאמען, קאנקרעטיזירט דורך געציילטע אפטיילונגען ווי די [[קאנטראווערסיע וועגן קאנטאר'ס געזעמלען טעאריע]], די [[בראוער-הילבערט קאנטראווערסיע]] און די [[בישאפ-קייזלער קאנטראווערסיע]]. | כדי צו געבן צו פארשטיין די [[פונדאמענטן פון מאטעמאטיק]] האט מען אנטוויקלט די געביטן פון [[מאטעמאטישע לאגיק|מאטעמאטישער לאגיק]] און [[געזעמלען טעאריע]], ווי אויך [[קאטעגאריע טעאריע]] וואס ווערט נאכאלץ אנטוויקלט. די פראזע "קריזיס פון פונדאמענטן" וואס באשרייבט די זוך אין אנהייב פונעם 20סטן יארהונדערט נאך פאסיקע פונדאמענטן פאר מאטעמאטיק, איז א פארציענדיקער פענאמען, קאנקרעטיזירט דורך געציילטע אפטיילונגען ווי די [[קאנטראווערסיע וועגן קאנטאר'ס געזעמלען טעאריע]], די [[בראוער-הילבערט קאנטראווערסיע]] און די [[בישאפ-קייזלער קאנטראווערסיע]]. | ||
מאטעמאטישע לאגיק באהאנדלט באזירן מאטעמאטיק אויף א פעסטער [[אקסיאם|אקסיאמאטישער]] ראם, און פארשט די רעזולטאטן פון דער ראם. דורך דעם קען מען דערגיין געדעל'ס [[צווייטער אומפולשטענדיקייט טעארעם|צווייטן אומפולשטענדיקייט טעארעם]], אפשר דער מערסט בארימטער רעזולטאט פון לאגיק, וואס ווייזט אן אין א נישט פארמאלן אופן אז יעדער [[מאטעמאטישער פארמאליזם]] וואס אנטהאלט | מאטעמאטישע לאגיק באהאנדלט באזירן מאטעמאטיק אויף א פעסטער [[אקסיאם|אקסיאמאטישער]] ראם, און פארשט די רעזולטאטן פון דער ראם. דורך דעם קען מען דערגיין געדעל'ס [[צווייטער אומפולשטענדיקייט טעארעם|צווייטן אומפולשטענדיקייט טעארעם]], אפשר דער מערסט בארימטער רעזולטאט פון לאגיק, וואס ווייזט אן אין א נישט פארמאלן אופן אז יעדער [[מאטעמאטישער פארמאליזם]] וואס אנטהאלט גרונטליכן אריטמעטיק, טאמער ער איז גענוג שטארק (דאס הייסט, אלע טעארעמן וואס מען קען באווייזן זענען געהעריג) מוז די סיסטעם זיין אומפולשטענדיק (דאס הייסט, אז עס זענען פארהאן געהעריגע טעארעמען וואס מען קען נישט באווייזן אין דער סיסטעם). מאדערנע לאגיק ווערט צעטיילט אויף [[רעקורסיע טעאריע]], [[מאדעלן טעאריע]] און [[באווייזן טעאריע]], און האט פעסטע פארהעלטענישן מיט טעארעטישער [[קאמפיוטער וויסנשאפט]]. | ||
:{| style="border:1px solid #ddd; text-align:center; margin: auto;" cellspacing="15" | :{| style="border:1px solid #ddd; text-align:center; margin: auto;" cellspacing="15" | ||
| שורה 122: | שורה 123: | ||
* [[העקס]] | * [[העקס]] | ||
* [[בעיס 64]] | * [[בעיס 64]] | ||
''' | '''באוואוסטע מאַטעמאַטיקער''' | ||
* [[רענע דעקארט]] | * [[רענע דעקארט]] | ||
* [[פיטאַגאָראַס]] | * [[פיטאַגאָראַס]] | ||
* [[ארכימעד]] | |||
* [[אוקלידוס]] | |||
* [[לעאנהארד אוילער|אוילער]] | |||
* [[יאהאן בערנולי]] | |||
* [[יאקאב בערנולי]] | |||
* [[דויד הילבערט]] | |||
* [[אנדרע קאלמאגאראוו]] | |||
* [[קורט גאדעל]] | |||
* [[געארג קאנטאר]] | |||
* [[וויליאם ראאן האמילטאן]] | |||
* [[זשאסעף פוריע]] | |||
==רעפערענצן== | ==רעפערענצן== | ||
| שורה 131: | שורה 143: | ||
[[קאַטעגאָריע:מאטעמאטיק|*]] | [[קאַטעגאָריע:מאטעמאטיק|*]] | ||
[[קאַטעגאָריע: | [[קאַטעגאָריע:אויף יידיש]] | ||
[[קאַטעגאָריע: | [[קאַטעגאָריע:נישט שלעכט]] | ||
[[קאַטעגאָריע:עלעמענטארע ארטיקלען צו פארברייטערן]] | |||
{{קרד/ויקי/יידיש}} | {{קרד/ויקי/יידיש}} | ||
[[he:מתמטיקה]] | |||
[[קאַטעגאָריע:וויקידאטא דעסקריפציע]] | |||
יעצטיגע רעוויזיע זינט 07:10, 11 פעברואר 2025
מאַטעמאַטיק איז די וויסנשאפט וואס פארנעמט זיך מיט צאלן און פארמען. מאטעמאטיק מיינט רעכענען, ציילן, און מעסטן. די אפטייל וואס באשעפטיגט זיך מיט פארמען און מאסן הייסט געאמעטריע. די וועג צו אויסגעפינען מאטעמאטיקס-פראבלעמען ווערט געטון דורך פארמולען.
דער וואס באשעפטיגט זיך מיט מאטעמאטיק, צי ווי א לערע אדער ווי א האבי, הייסט א מאטעמאטיקער.
אין אקאדעמיע, איז מאטעמאטיק אן אפטייל פון די פינקטליכע וויסנשאפט. מיט די לערע קען מען פארשן פיזיק, כעמיע, אסטראנאמיע, סטאטיסטיק און נאך. אויך אין דעם לעבנסשטייגער ניצט מען זיך מיט מאטעמאטיק אויף האנדל און ביזנעס.
קארל פרידריך גאוס (1777–1855) האט גערופן מאטעמאטיק "די מלכה פון די וויסנשאפטן".
מאטעמאטיק איז אינטערעסירט אין נומערן, סטרוקטור, פארעם און ענדערונג. מען שטודירט זיי מיט לאגיק צו שאפן אלגעמיינע כללים פון וואס מען קען אויסלערנען נייע רעזולטאטן.
מאטעמאטיק אנטוויקלט זיך דורך דריי כאראקטעריסטיקן: אבסטראקציע, גענעראליזאציע און דערווייז.
מאטעמאטיק איז א לעבנסנויטיגער געצייג אין פארשידענע געביטן, איינשליסנדיק נאטור-וויסנשאפטן, אינזשעניריע, מעדיצין און געוויסע סאציאל וויסנשאפטן ווי עקאנאמיק און פסיכאלאגיע. פראבלעמען וואס שטאמען פון אנדערע וויסנשאפט צווייגן זענען א קאטאליזאטאר פאר נייע מאטעמאטיקע אויסגעפינען, און טיילמאל אפילו נייע מאטעמאטישע געביטן. אנגעווענדעטע מאטעמאטיק, די צווייג פון מאטעמאטיק וואס באהאנדלט די אנווענדונג פון מאטעמאטישן וויסן צו אנדערע פעלדער, אינספירירט און ניצט נייע מאטעמאטישע אויספינדונגען, ברענגנדיק די אנטוויקלונג פון נייע מאטעמאטישע דיסציפלינען, ווי למשל סטאטיסטיק און שפיל טעאריע. אויך פארנעמען זיך מאטעמאטיקער מיט ריינע מאטעמאטיק, אן קיין שום קלער פון אן אנווענדונג.
עטימאלאגיע
דאס ווארט "מאטעמאטיק" (גריכיש: μαθηματικά) שטאמט פון גריכיש [μάθημα [máthēma וואס מיינט לערנען, שטודירן, און אויך די מער באגרעניצט און טעכנישערע באדייטונג "שטודירן מאטעמאטיק".
אין זיין איבערזעצונג פונעם רמב"מ'ס מורה נבוכים, אנהייב פונעם 13טן יארהונדערט, ניצט הרב שמואל איבן תיבון דאס ווארט "לימודיים" פאר מאטעמאטיק, וואס איז א גלייכע אפטייטש פון גריכיש.
היסטאריע
די בבליים און די מצריים האבן געניצט אריטמעטיק, אלגעברע און געאמעטריע פאר באשטייערונג און אנדערע פינאנציעלע חשבונות, פאר בויען און קאנסטרוקציע, און פאר אסטראנאמיע.[1] די ערשטע באניצן פון מאטעמאטיק זענען געווען אין האנדל, ערד־מעסטן, מאלעריי און וועבן מוסטערן און אין רעכענען צייט. די בבליים און מצריים האבן געהאט א ידיעה וועגן קוואדראטישע גלייכונגען, קוואדראט ווארצלען און שטח פון פלאכע פיגורן.
נייע מאטעמאטישע אויסגעפינען זענען געווארן אנטדעקט דורכאויס דער היסטאריע, און ווערן נאכאלץ אנטדעקט ביזן היינטיגן טאג. די אנטוויקלונג פון מאטעמאטיק אין אוראלטע צייטן האט דערגרייכט איר שפיץ און אוראלט גריכנלאנד, א דאנק די בארימטע מאטעמאטיקער ווי אוקלידוס און ארכימעד. אין דעם מיטל אלטער איז די עיקר אנטוויקלונג געווען ביי די אראבער, וואס האבן אנטוויקלט אלגעברע און טריגאנאמעטריע. אינעם 17טן יארהונדערט האבן געבליט פארשידענע צווייגן פון מאטעמאטיק, למשל אנאליטישע געאמעטריע און קאלקולוס, וואס זענען געווארן די שפרינגברעט פאר פיל וויסנשאפטליכע צווייגן. די אנטוויקלונג פון נישט-אוקלידישער געאמעטריע אינעם 19טן יארהונדערט האבן אונטערגעשריכן די וויכטיגקייט פון אקסיאמען אין מאטעמאטיק, אין די פארווייטערונג פון אן אינטואיטיוון צוגאנג. בים סוף פונעם 19טן יארהונדערט איז אנטוויקלט געווארן געזעמלען טעאריע, און אויך האט אנטוויקלט א דעבאטע וועגן די פונדאמענטן פון מאטעמאטיק. אינעם 20סטן יארהונדערט האט מאטעמאטיק זיך אנטוויקלט גיך, מיט דער לייזונג פון מערערע פון הילבערטס 23 פראבלעמען.
מאטעמאטישע סימבאלן
די מאטעמאטישע סימבאלן וואס ווערן געניצט היינט זענען מערסטנס נאר פונעם 16טן יארהונדערט און שפעטער. פריער פלעג מען שרייבן מאטעמאטיק נאר מיט ווערטער אן סימבאלן. אינעם 18טן יארהונטדערט האט לעאנהארד אוילער דערפינדעט א סך פון די סימבאלן וואס מען ניצט היינט. מיט סימבאלן קען מען בעסער און גיכער אנטוויקלען מאטעמאטיק, כאטש נייע באניצער דארפן אויסלערנען וויאזוי מען ניצט די סימבאלן. מאטעמאטישער סימבאליזם איז זייער אנגעפאקט: מיט די סימבאלן איז מעגלעך גאנץ אין קורצן אויסצושפרעכן א סך אינפארמאציע.
אפילו די שפראך פון מאטעמאטיק קען זיין שווער פאר אנהייבער צו פארשטיין. אזא פשוט ווארט ווי "אדער" האט א ספעציפישן באדייט אין מאטעמאטיק. אויסער דעם ניצן מאטעמאטיקער ווערטער ווי "אפן" און "פעלד" מיט א באזונדערער מאטעמאטישער באדייטונג. אין מאטעמאטיק דארף אלץ זיין פינקטלעך, וואס מאטעמאטיקער רופן שטרענגקייט.
כדי צו פארמיידן אויסרעדן טעראמען וואס זענען נישט גוט אויסגעהאלטן פירן זיך מאטעמאטיקער אוועקלייגן א פונדאציע פון אקסיאמען פון וואס מען קען ארויספירן נייע אייגנשאפטן.
וועגן מאטעמאטיק
מאטעמאטיק ווערט געניצט צו לייזן פראבלעמען וועגן נומער (קוואנטיטעט), סטרוקטור, פארעם אדער ענדערונג. אריגינעל האבן די פראבלעמען געשטאמט פון האנדל, פון מעסטן ערטער און פון אסטראנאמיע; היינט אבער שטאמען מאטעמאטישע פראבלעמען פון אלע וויסנשאפטן און אויך פון מאטעמאטיק אליין. דער פיזיקער יוזשין וויגנער האט באמערקט אז גאנץ אפט האט א געדאנק פון ריינעם מאטעמאטיק א פראקטישע אפליקאציע, למשל, נומערן טעאריע אין קריפטאגראפיע.
כמות
די שטודיע פון כמות (קוואַנטיטעט) הייבט אן מיט נומערן, ערשט די באקאנטע נאטירליכע צאל און גאנצע צאל, מיט די אריטמעטישע אפעראציעס אויף זיי, וואס צוזאמען ווערן שטודירט אין אריטמעטיק. די טיפערע אייגנשאפטן פון נומערן שטודירט מען אין נומערן טעאריע, פון וואנעט קומען אזעלכע רעזולטאטן ווי פערמא'ס לעצטער טעארעם. צווישן די נישט געלייזטע פראבלעמען פון נומערן טעאריע זענען די פרימצאל-צווילינג השערה און די גאלדבאך-השערה.
מיט דער אנטוויקלונג פון דער נומערן־סיסטעם, אנערקענט מען די נאטירליכע צאל ווי אן אונטער־געזעמל פון די ראציאנאלע צאל (בראכטיילן), וואס זיי זענען א טייל פון די רעאלע צאל, מיט וואס מען קען דעפינירן נאכאנאנדיקע פונקציעס. רעאלע צאל קען מען פארברייטערן ווייטער צו קאמפלעקסע צאל.
סטרוקטור
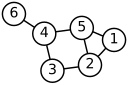
א סך מאטעמאטישע אביעקטן, ווי סכומען פון נומערן און פונקציעס, ווייזן אינווייניקע סטרוקטור.
ביישפילן פון געביטן אין מאטעמאטיק וואס באהאנדלען סטרוקטור זענען:
פארעם
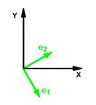
די שטודיע פון פארעם און רוים הייבט אן מיט געאמעטריע, ספעציעל אויקלידישע געאמעטריע. די מאדערנע שטודיע פון געאמעטריע גענעראליזירט צו געאמעטריע אין מערערע דימענסיעס, נישט-אויקלידישע געאמעטריע (וואס שפילט א צענטראל ראלע אין אלגעמיינער רעלאטיוויטעט) און טאפאלאגיע. אנדערע געביטן פון מאטעמאטיק וואס באהאנדלען פארעם זענען אנאליטישע געאמעטריע, דיפערענציאלע געאמעטריע און אלגעברעאישע געאמעטריע. אין דיפערענציאלער געאמעטריע געפינען זיך די באגריפן פון פיבערבינטלעך און קאלקולוס אויף פלאכטעס, ספעציעל וועקטאר און טענסאר קאלקולוס.
די שטודיע פון אויקלידישע געאמעטריע שליסט איין דעם בארימטן פיטאגאראס פרינציפ און טריגאנאמעטריע, וואס באהאנדלט די פארהעלטענישן צווישן די זייטן און ווינקלען פון דרייעקן און מיט די טריגאנאמעטרישע פונקציעס.
אין געאמעטרישער אלגעברע ווערן געאמעטרישע אביעקטן באשריבן ווי געזעמלען פון לייזונגען פון פאלינאמישע גלייכונגען, און אזוי ווערן איינגעפלאכטן די באגריפן פון כמות און פארעם; אויך פארשט מען טאפאלאגישע גרופעס וואס פלעכטן איין סטרוקטור און פארעם. לי גרופעס דינען צו פארשן פארעם, סטרוקטור און ענדערונג. טאפאלאגיע, מיט אירע אונטערצווייגן, איז געווען דער געביט מיט דער גרעסטער אנטוויקלונג אינעם 20סטן יארהונדערט, און שליסט איין די פואנקארע השערה און דעם פיר-פארבן טעארעם, וואס איז געווארן אויפגעוויזן מיטן הילף פון א קאמפיוטער און קיין שום מענטש האט נאך נישט באשטעטיקט זיין ריכטיקייט.
ענדערונג
שילדערן און פארשטיין ענדערונג איז שטארק נויטבאר אין דער נאטור-וויסנשאפטן, און דער קאלקולוס איז א קראפטיגער געצייג דערפאר. דער הויפט באגריף איז די פונקציע. די שטודיע פון רעאלע צאלן און פונקציעס וואס האבן רעאלע ווערטן הייסט רעאלער אנאליז, און די פאראלעלע שטודיע פון פונקציעס פון קאמפלעקסע צאלן הייסט קאמפלעקסער אנאליז. די רימאן השערה, איינע פון די אפענע יסודותדיקע פראגעס אין מאטעמאטיק, קוואלט ארויס פון קאמפלעקסן אנאליז. פונקציאנאלער אנאליז פאקוסירט אויף פונקציע רוימען, בדרך כלל מיט אומענדליכע דימענסיעס. פונקציאנאלער אנאליז ווערט געניצט אין קוואנטן-מעכאניק. עס זענען פאראן פילע פראבלעמען וואס זייער לייזונג ליגט אין א פארהעלטעניש צווישן א קוואנטיטעט און זיין ענדערונג, וואס מען שטודירט אין דעם געביט פון דיפערענציאל-גלייכונגען.
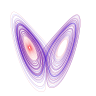
א סך פענאמענען אין נאטור קען מען שילדערן דורך דינאמישע סיסטעמען; כאאס-טעאריע פארשט גענוי ווי די סיסטעמען ארבעטן. נומערישער אנאליז פארשט מעטאדן צו לייזן א ברייטן גרייך פון פראבלעמען וואס מען קען נישט לייזן אנאליטיש.
 |
 |
 |

|
| קאלקולוס | וועקטאר-אנאליז | דיפערענציאלע גלייכונגען | דינאמישע סיסטעמען |
 |
 |
 |
|
| כאאס טעאריע | נומערישער אנאליז | מאטעמאטישע פיזיק | שטראמען מעכאניק |
פונדאמענטן און פילאזאפיע
כדי צו געבן צו פארשטיין די פונדאמענטן פון מאטעמאטיק האט מען אנטוויקלט די געביטן פון מאטעמאטישער לאגיק און געזעמלען טעאריע, ווי אויך קאטעגאריע טעאריע וואס ווערט נאכאלץ אנטוויקלט. די פראזע "קריזיס פון פונדאמענטן" וואס באשרייבט די זוך אין אנהייב פונעם 20סטן יארהונדערט נאך פאסיקע פונדאמענטן פאר מאטעמאטיק, איז א פארציענדיקער פענאמען, קאנקרעטיזירט דורך געציילטע אפטיילונגען ווי די קאנטראווערסיע וועגן קאנטאר'ס געזעמלען טעאריע, די בראוער-הילבערט קאנטראווערסיע און די בישאפ-קייזלער קאנטראווערסיע.
מאטעמאטישע לאגיק באהאנדלט באזירן מאטעמאטיק אויף א פעסטער אקסיאמאטישער ראם, און פארשט די רעזולטאטן פון דער ראם. דורך דעם קען מען דערגיין געדעל'ס צווייטן אומפולשטענדיקייט טעארעם, אפשר דער מערסט בארימטער רעזולטאט פון לאגיק, וואס ווייזט אן אין א נישט פארמאלן אופן אז יעדער מאטעמאטישער פארמאליזם וואס אנטהאלט גרונטליכן אריטמעטיק, טאמער ער איז גענוג שטארק (דאס הייסט, אלע טעארעמן וואס מען קען באווייזן זענען געהעריג) מוז די סיסטעם זיין אומפולשטענדיק (דאס הייסט, אז עס זענען פארהאן געהעריגע טעארעמען וואס מען קען נישט באווייזן אין דער סיסטעם). מאדערנע לאגיק ווערט צעטיילט אויף רעקורסיע טעאריע, מאדעלן טעאריע און באווייזן טעאריע, און האט פעסטע פארהעלטענישן מיט טעארעטישער קאמפיוטער וויסנשאפט.
דיסקרעטע מאטעמאטיק
דיסקרעטע מאטעמאטיק איז א ברייטער געביט פון מאטעמאטיק וואס באשעפטיגט זיך מיט פארשן די נאטור פון דיסקרעטע מאטעמאטיקע סטרוקטורן (אנדערש ווי מאטעמאטישער אנאליז, וואס באהאנדלט המשכדיקע מאטעמאטישע סטרוקטורן). די אביעקטן וואס מען שטודירט אין דיסטקרעטער מאטעמאטיק זענען מערסטנס צייליקע געזעמלען.
דיסקרעטע מאטעמאטיק איז געווארן זייער פאפולער זייט דעם צווייטן העלפט פונעם 20סטן יארהונדערט, א דאנק איר ניץ אין קאמפיוטער-וויסנשאַפט: א דיגיטאלישע קאמפיוטער (אנדערש ווי אן אנאלאג קאמפיוטער) ארבעט דיסקרעטיש, א טריט נאך א טריט, דערפאר איז דיסקרעטע מאטעמאטיק שטארק רעלעוואנט צו די טעארעטישע פונדאמענטן פון זיין ארבעט.
די הויפט צווייגן וואס ווערן איינגעשלאסן אין דער ברייטערער ראם פון דיסקרעטער מאטעמאטיק זענען: קאמבינאטאריק, גראפן-טעאריע, אלגאריטמיק און ובולעשע אלגעברע.
זעט אויך
באוואוסטע מאַטעמאַטיקער
- רענע דעקארט
- פיטאַגאָראַס
- ארכימעד
- אוקלידוס
- אוילער
- יאהאן בערנולי
- יאקאב בערנולי
- דויד הילבערט
- אנדרע קאלמאגאראוו
- קורט גאדעל
- געארג קאנטאר
- וויליאם ראאן האמילטאן
- זשאסעף פוריע
רעפערענצן
- ↑ Kline 1990, Chapter 1.
דאס איז נישט קיין המכלול ארטיקל, בלויז עפעס וואס ליגט דא ביז עס וועט ערזעצט ווערן מיט בעסערס. שרייבט עס איבער!