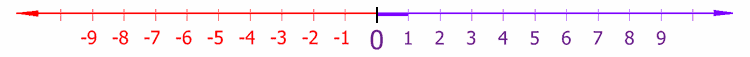אונטערשייד צווישן ווערסיעס פון "רוי:קאארדינאטן סיסטעם"
ק (החלפת טקסט – "קאַטעגאָריע:וויקידאטא שפראכן דעסקריפציע" ב־"") |
ק (החלפת טקסט – "{{דעסקריפציע||ענגליש=" ב־"{{דעסקריפציע||ענגליש = ") |
||
| שורה 1: | שורה 1: | ||
{{דעסקריפציע||ענגליש=system for determining the position of a point|העב=שיטה לייצוג מיקום במרחב|דייטש=Beschreibung der Position von Punkten|}} | {{דעסקריפציע||ענגליש = system for determining the position of a point|העב=שיטה לייצוג מיקום במרחב|דייטש=Beschreibung der Position von Punkten|}} | ||
אין [[געאמעטריע]] איז א '''קאארדינאַטן סיסטעם''' א סיסטעם וואס באניצט איין אדער מער [[נומער]]ן, וואס מען רופט '''קאארדינאטן''', צו באשטימען איינציק די פלאצירונג פון א [[פונקט (געאמעטריע)|פונקט]] אדער אן אנדער געאמעטרישן עלעמענט.<ref>Woods p. 1</ref><ref>[[Eric W. Weisstein|Weisstein, Eric W.]], "[http://mathworld.wolfram.com/CoordinateSystem.html קאארדינאטן סיסטעם]" פון [[MathWorld]]</ref> דער סדר פון די קאארדינאטן איז דייטיק—טיילמאל אידענטיפירט מען א קאארדינאט מיט זיין פאזיציע אין דעם סדר און טיילמאל מיט א בוכשטאב, ווי למשל 'דער ''x''-קאארדינאט'. אין עלעמענטארן מאטעמאטיק זענען די קאארדינאטן [[רעאלע צאל]]ן, אבער אין מער פארגעשריטענע אנווענדונגען קענען די קאארדינאטן זיין אדער [[קאמפלעקסע צאל]]ן אדער די עלעמענטן פון א מער אבסטראקטער סיסטעם ווי א [[קאמוטאטיווער רינג]]. מיטן ניץ פון א קאארדינאטן סיסטעם קען מען איבערזעצן פראבלעמען אין געאמעטריע אויף פראבלעמען וועגן נומערן און פארקערט; דאס איז דער יסוד פון [[אנאליטישע געאמעטריע|אנאליטישער געאמעטריע]].<ref> | אין [[געאמעטריע]] איז א '''קאארדינאַטן סיסטעם''' א סיסטעם וואס באניצט איין אדער מער [[נומער]]ן, וואס מען רופט '''קאארדינאטן''', צו באשטימען איינציק די פלאצירונג פון א [[פונקט (געאמעטריע)|פונקט]] אדער אן אנדער געאמעטרישן עלעמענט.<ref>Woods p. 1</ref><ref>[[Eric W. Weisstein|Weisstein, Eric W.]], "[http://mathworld.wolfram.com/CoordinateSystem.html קאארדינאטן סיסטעם]" פון [[MathWorld]]</ref> דער סדר פון די קאארדינאטן איז דייטיק—טיילמאל אידענטיפירט מען א קאארדינאט מיט זיין פאזיציע אין דעם סדר און טיילמאל מיט א בוכשטאב, ווי למשל 'דער ''x''-קאארדינאט'. אין עלעמענטארן מאטעמאטיק זענען די קאארדינאטן [[רעאלע צאל]]ן, אבער אין מער פארגעשריטענע אנווענדונגען קענען די קאארדינאטן זיין אדער [[קאמפלעקסע צאל]]ן אדער די עלעמענטן פון א מער אבסטראקטער סיסטעם ווי א [[קאמוטאטיווער רינג]]. מיטן ניץ פון א קאארדינאטן סיסטעם קען מען איבערזעצן פראבלעמען אין געאמעטריע אויף פראבלעמען וועגן נומערן און פארקערט; דאס איז דער יסוד פון [[אנאליטישע געאמעטריע|אנאליטישער געאמעטריע]].<ref> | ||
[[Eric W. Weisstein|Weisstein, Eric W.]], "[http://mathworld.wolfram.com/Coordinates.html קאארדינאטן]" פון [[MathWorld]]</ref> | [[Eric W. Weisstein|Weisstein, Eric W.]], "[http://mathworld.wolfram.com/Coordinates.html קאארדינאטן]" פון [[MathWorld]]</ref> | ||
יעצטיגע רעוויזיע זינט 22:08, 26 אקטאבער 2023
אין געאמעטריע איז א קאארדינאַטן סיסטעם א סיסטעם וואס באניצט איין אדער מער נומערן, וואס מען רופט קאארדינאטן, צו באשטימען איינציק די פלאצירונג פון א פונקט אדער אן אנדער געאמעטרישן עלעמענט.[1][2] דער סדר פון די קאארדינאטן איז דייטיק—טיילמאל אידענטיפירט מען א קאארדינאט מיט זיין פאזיציע אין דעם סדר און טיילמאל מיט א בוכשטאב, ווי למשל 'דער x-קאארדינאט'. אין עלעמענטארן מאטעמאטיק זענען די קאארדינאטן רעאלע צאלן, אבער אין מער פארגעשריטענע אנווענדונגען קענען די קאארדינאטן זיין אדער קאמפלעקסע צאלן אדער די עלעמענטן פון א מער אבסטראקטער סיסטעם ווי א קאמוטאטיווער רינג. מיטן ניץ פון א קאארדינאטן סיסטעם קען מען איבערזעצן פראבלעמען אין געאמעטריע אויף פראבלעמען וועגן נומערן און פארקערט; דאס איז דער יסוד פון אנאליטישער געאמעטריע.[3]
א דוגמא וואס מען ניצט אין טאג־טעגליכן לעבן איז די סיסטעם פון געבן א ברייט און לענג צו געאגראפישע ערטער.
נומערן ליניע
{דער פשוטסטער ביישפיל פון א קאארדינאטן סיסטעם איז די אידענטיפיקאציע פון פונקטן אויף א ליניע מיט רעאלע צאלן, ניצנדיק די נומערן ליניע. אין דער דאזיגער סיסטעם, קלויבט מען אויס נארוועלכע פונקט O פאר 0 (נול) אויף דער געגעבענער ליניע. דער קאארדינאט פון א פונקט P איז דער דיסטאנץ פון O ביז P, און מען מעסט דעם דיסטאנץ נעגאטיוו ווען P איז לינקס פון O. יעדער פונקט האט אן איינציקן קאארדינאט, און יעדע רעאלע צאל איז דער קאארדינאט פון אן איינציקן פונקט.[4]
קארטעזישע קאארדינאטן סיסטעם

דער טיפישער ביישפיל פון א קאארדינאטן סיסטעם איז די קארטעזישע קאארדינאטן סיסטעם, אין דער פלאך, קלויבט מען אויס צוויי פערפענדיקולארע ליניעס, און די קאארדינאטן פון א פונקט זענען די געצייכנטע דיסטאנצן ביז די ליניעס.
אין דריי דימענסיעס, קלויבט מען אויס דריי פלאכן וואס זענען פערפענדיקולאר מיט אנאנד, און די דריי קאארדינאטן פון א פונקט זענען די געצייכנטע דיסטאנצן ביז יעדן איינעם פון די פלאכן. דאס קען מען גענעראליזירן צו שאפן n קאארדינאטן פאר אבי וועלכן פונקט אין n-דימענסיאנאלן אוקלידאנעם רוים.
זעט אויך
רעפערענצן
- ↑ Woods p. 1
- ↑ Weisstein, Eric W., "קאארדינאטן סיסטעם" פון MathWorld
- ↑ Weisstein, Eric W., "קאארדינאטן" פון MathWorld
- ↑ Woods p. 8
- Woods, Frederick S. (1922). Higher Geometry. Ginn and Co. pp. 1ff
דאס איז נישט קיין המכלול ארטיקל, בלויז עפעס וואס ליגט דא ביז עס וועט ערזעצט ווערן מיט בעסערס. שרייבט עס איבער!